다이나믹 프로그래밍.
동적 계획법.
내가 지금 이걸 왜 배워야 하는데?
대표적인 알고리즘 설계 기법이
그리디, 디바이드앤컹쿼(ㅋ), 다이나믹 프로그래밍이다.
기본이니까 배워야지!
프로그래머스 레벨2 정도에 오니까 인덱스 가지고 배열을 요리조리 돌려서 문제 푸는 걸로는 안 된다.
한 예를 들어 보겠다.
https://school.programmers.co.kr/learn/courses/30/lessons/12945
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
난 이 문제를 아래와 같이 풀었다.
class Solution {
public int solution(int n) {
return (int) fibonacci(n) % 1234567;
}
private int fibonacci(int n) {
if(n==0) return 0;
if(n==1) return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
}적당~히 될 것 같은데
어림도 없지!

레벨2부터는 적당~히 풀면 코드 제출이 안 된다.
그래서 이제 진짜... '배워야' 하는 단계에 온 거다.
무엇을? 알고리즘을.
런타임 에러가 난 것에 대해 프로그래머스에서는
https://school.programmers.co.kr/learn/courses/14743/lessons/116433
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
다음과 같이 솔루션을 제시한다.
결론은 '점화식 쓰면 런타임 에러 나니까 동적 프로그래밍으로 푸세요~'다.
그래서 동적 프로그래밍이 뭔데?
동적 프로그래밍(DP)은 큰 문제를 작은 하위 문제로 나누고, 그 하위 문제들의 결과를 저장해 재사용함으로써 문제를 효율적으로 해결하는 알고리즘 기법이다.
https://www.geeksforgeeks.org/dynamic-programming/
Dynamic Programming or DP - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
DP로 들어가니까 바로 피보나치 관련 코드가 나오네.

느낌은 온다.
재귀적인 점화식을 사용하면 일반적으로 중복 계산이 발생할 수 있다고 한다.
그래서 느리니까 DP 쓰라는 건데, 어떻게 그럴까?
앞의 피보나치 수열의 점화식을 다시 보자.
n이 5라고 치면
fibonacci(5)
= fibonacci(4) + fibonacci(3)
fibonacci(4)
= fibonacci(3) + fibonacci(2) // 여기서 fibonacci(2) 한 번
fibonacci(3)
= fibonacci(2) + fibonacci(1) // 여기서 fibonacci(2) 한 번
다른 fibonacci(3) (첫 번째 줄에서 두 번째 fibonacci(3) 호출)
= fibonacci(2) + fibonacci(1) // 여기서 fibonacci(2) 또 한 번
총 세 번:
fibonacci(2) (fibonacci(4)에서)
fibonacci(2) (첫 번째 fibonacci(3)에서)
fibonacci(2) (두 번째 fibonacci(3)에서)이러하다.
fib(3)은 두 번 계산되고, fib(2)는 세 번 계산된다.
이렇게 동일한 함수를 중복해서 호출하면 컴퓨팅 성능이 저하된다.
DP는 분할, 저장, 조합을 통해 위와 같은 문제를 피한다.
분할: 문제를 작은 하위 문제로 나눈다.
저장: 하위 문제의 결과를 저장해 두어 중복 계산을 피한다.
조합: 하위 문제들의 결과를 조합하여 전체 문제를 해결한다.
DP는 탑다운 or 바텁업 방식으로 구현할 수 있다.
탑다운: 재귀를 사용해서, 계산된 결과를 메뫄제이션(ㅋ) 기법을 통해 저장한다.
Memoization... 메모이제이션...?; OK. 메모이제이션!!!
바텁업: 반복문을 사용하여 작은 하위 문제부터 차례로 해결한다. 그리고 그 결과를 저장해 전체 문제를 해결한다.
아니 그래서 피보나치 문제 DP로 어떻게 푸냐고요...
import java.util.HashMap;
import java.util.Map;
class Solution {
private Map<Integer, Long> memo = new HashMap<>();
public int solution(int n) {
// 최종 결과에 대해 모듈로 연산을 적용하여 int로 캐스팅하여 반환합니다.
return (int) (fibonacci(n) % 1234567);
}
private long fibonacci(int n) {
// 기본 조건: n이 0 또는 1일 때 결과 반환
if (n == 0) return 0;
if (n == 1) return 1;
// 이미 계산된 값이 memo에 있으면 해당 값 반환
if (memo.containsKey(n)) return memo.get(n);
// 재귀적으로 피보나치 값을 계산하고, 모듈로 연산을 통해 값의 크기를 제한
long result = (fibonacci(n - 1) + fibonacci(n - 2)) % 1234567;
// 계산된 값을 memo에 저장
memo.put(n, result);
// 결과 반환
return result;
}
}이 문제가 순수 피보나치 수열을 구하라는 건 아니고,
모듈로 연산 값을 int 형식으로 반환하라는 거니까,
if (memo.containsKey(n)) ~ 같은 코드가 붙는 것.
그런데 이 코드로도 13번 테스트 케이스 통과가 안 된다.
너무 심각하게 생각할 것 없이 바텀업 방식을 적용해 보자.
* 참고 *
모듈러(Modular) 아니다.
모듈로(Modulo)다.
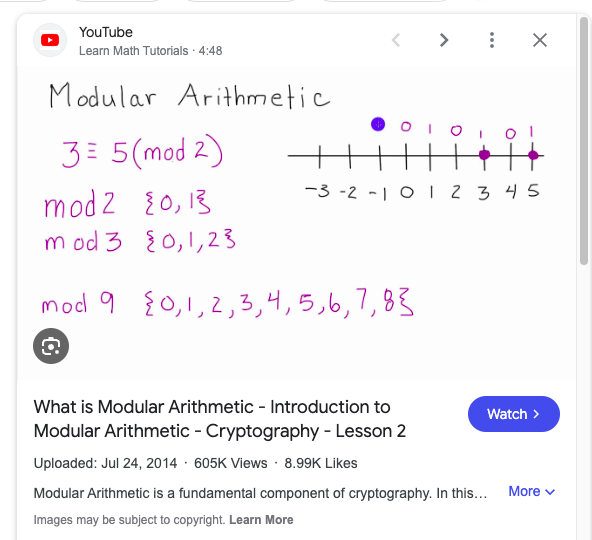
완전 다름...
아무튼, 바텀업 가자.
class Solution {
public int solution(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
long[] dp = new long[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % 1234567;
}
return (int) dp[n];
}
}와!
탑다운 형식으로 안 되던 거 바텀업으로 하니까 된다!
그런데 내가 이 코드를 처음 봤을 때 든 생각이
'이게 왜 DP라는 걸까...?'였다.

요거 때문에 그러는 것 같긴 한데 크게 느낌이 안 왔다.
그래도 계속 코드를 보니
dp[2], dp[3] 등에 해당하는 값을 배열에 바로 바로 박아 놓고 있는 걸 알게 됐다.
그러면 인덱스만 알면 O(1)로 값 조회가 바로 되겠지.
바텀업 방식은...
1. 부분 문제를 재사용해서 좋다.
2. 이 방식은 각 피보나치 수를 한 번씩만 계산하니까 시간 복잡도가 O(N)이다.
안 쓸 이유가 없다.
3. 공간 복잡도는 O(N)이지만 변수를 두 개만 사용해서 O(1)로 최적화할 수도 있다.
여기서는 일단 이 정도만 이해한다!
골든래빗 출판사의 묘공단 스터디를 진행하며
코딩 테스트 합격자 되기 - 자바 편 프로그래머스 제공 97 문제로 완벽 대비를 읽고 정리한 내용입니다.
'코딩테스트 연습' 카테고리의 다른 글
| 점프와 순간 이동 (0) | 2024.05.27 |
|---|---|
| [묘공단] 완전 탐색이란? (0) | 2024.05.20 |
| [묘공단] 너비 우선 탐색(BFS) (0) | 2024.05.19 |
| [묘공단] 깊이 우선 탐색(DFS) (0) | 2024.05.19 |
| 다음 큰 숫자 (2) | 2024.05.12 |



