https://school.programmers.co.kr/learn/courses/30/lessons/12911
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
때가 되었다...
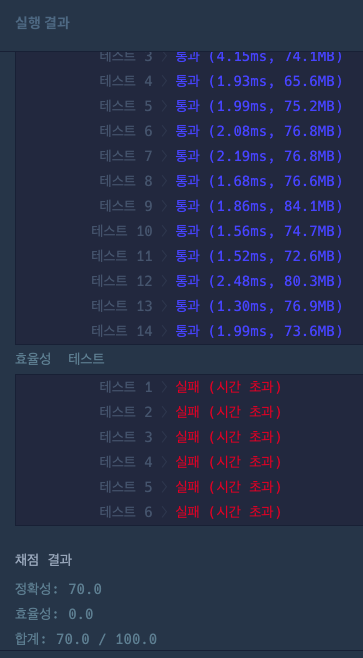
이제는 정확성이 100%여도 효율성이 떨어져서 코드 통과 못 하는 지점에 왔다.
import java.util.stream.*;
class Solution {
public int solution(int n) {
String bn1 = "", bn2 = "";
int bn1Length = 0, bn2Length = 0;
long bn11s = 0, bn21s = 0;
int answer = 0;
bn1 = Integer.toBinaryString(n);
final String finalbn1 = bn1;
bn1Length = bn1.length();
bn11s = IntStream.range(0,bn1Length)
.filter(i -> finalbn1.charAt(i) == '1')
.count();
for(int i=n+1; i<=1000000; i++) {
bn2 = Integer.toBinaryString(i);
final String finalbn2 = bn2;
bn2Length = bn2.length();
bn21s = IntStream.range(0,bn2Length)
.filter(k -> finalbn2.charAt(k) == '1')
.count();
if(bn11s == bn21s) {
answer = i;
break;
}
}
return answer;
}
}내가 제출한 코드는 이러하다.
효율성까지 생각하면서 코딩하는 건 지금 못 하겠으니까 정확도가 100%인 상태에서 리팩토링을 해 보자.
> ...리팩토링을 했는데 해결이 안 됐다.
GPT와 대화를 나누었고 두 종류의 코드를 받았다.
둘 다 비트 연산자를 활용하는 방법이었다.
이진수가 들어간 문제라면 비트 연산자를 활용하는 게 맞다고 생각한다.
게다가 본 문제에서는 다루는 수가 백만까지 갈 수도 있어 더욱 비트 연산자를 활용하는 게 맞다고 생각은 한다만
코테를 치르는 중에 비트 연산자를 잘 못 활용할 수도 있잖아?
이 문제가 정말로 비트 연산자를 쓰지 않으면 풀 수 없는 문제인가?
네, 여러분이 제시한 문제와 같은 이진수 처리나 비트 카운트 문제에서는 비트 연산자를 사용하는 것이 매우 효율적인 접근 방법입니다. 비트 연산을 활용하지 않고 해결하려고 하면, 일반적으로 처리해야 할 단계가 더 많고, 코드도 더 복잡해지며, 실행 시간도 길어질 가능성이 큽니다.
비트 연산의 중요성
비트 연산자를 사용하는 것은 다음과 같은 이유로 중요합니다:
- 효율성: 비트 연산은 CPU 수준에서 직접 지원되므로 매우 빠르고 효율적입니다. 이진수 표현에 직접 작업을 할 때 특히 유리합니다.
- 간결성: 비트 연산을 사용하면 복잡한 루프나 조건문 없이도 데이터의 비트 수준에서 직접 조작이 가능해 코드가 간결해집니다.
- 직관성: 이진수 처리에 있어서 비트 연산은 문제의 본질과 가장 직관적으로 매치되기 때문에 문제 해결에 있어 직관적인 접근을 가능하게 합니다.
비트 연산 없이 문제 해결
비트 연산을 사용하지 않고 이 문제를 해결하려면, 일반적으로 문자열 처리나 수학적 계산을 사용해야 합니다. 예를 들어:
- 문자열 변환과 반복문: 숫자를 이진 문자열로 변환한 다음, 문자열을 반복하여 '1'의 개수를 세는 방법을 사용할 수 있습니다. 하지만 이 방법은 문자열 생성과 가비지 컬렉션 비용 때문에 효율적이지 않습니다.
- 재귀나 반복문을 이용한 수학적 계산: 숫자를 반복적으로 나누어 '1'의 개수를 세는 방법을 사용할 수 있지만, 이 역시 비트 연산에 비해 느립니다.
결론
비트 연산을 활용하는 것은 이진수 관련 문제를 해결하기 위한 최적의 방법 중 하나입니다. 코딩 테스트나 시스템 프로그래밍에서 비트 연산을 잘 이해하고 사용하는 것은 매우 중요합니다. 만약 비트 연산에 익숙하지 않다면, 이를 연습하고 익숙해지는 것이 좋습니다.
일단 나부터가 효율성 때문에 코드 통과를 못 했다.
그러니 이제는 그냥 앞으로 비트 연산자 사용을 적극적으로 해 보는 수밖에 없구나 싶다.
문제 푸는 방식 1번을 보자.
> 제공하신 코드에서 Integer.toBinaryString(i)와 스트림을 이용한 '1'의 개수 세기는 각 반복마다 비교적 높은 시간 복잡도를 가지고 있어, 특히 n이 큰 범위로 가게 될 때 이는 성능 문제로 이어집니다. 효율성을 개선하기 위해서는 다음과 같은 접근을 고려할 수 있습니다:
1. 비트 연산 사용
비트 연산을 사용하여 숫자의 이진 표현에서 '1'의 개수를 세는 방법은 표준 라이브러리 함수를 호출하는 것보다 훨씬 빠를 수 있습니다. Java에는 Integer.bitCount() 메소드가 있으며, 이는 정수의 이진 표현에서 1의 개수를 직접 반환합니다.
class Solution {
public int solution(int n) {
int answer = 0;
long bn11s = Integer.bitCount(n);
for(int i = n + 1; i <= 1000000; i++) {
long bn21s = Integer.bitCount(i);
if (bn11s == bn21s) {
answer = i;
break;
}
}
return answer;
}
}2. 최적화된 탐색 방법
현재 코드는 n+1부터 1000000까지 모든 숫자를 이진 변환하고 '1'의 개수를 세며, 조건에 맞는 숫자를 찾을 때까지 반복합니다. 이 접근 방식은 최악의 경우 매우 많은 계산을 필요로 합니다. 최적화를 위해서는 다음과 같은 접근이 가능합니다:
- 이진 표현의 '1'의 수를 빠르게 증가시키기: '1'의 개수를 조절하여 목표하는 이진 표현의 '1' 개수에 더 빠르게 접근할 수 있는 방법을 고려합니다. 예를 들어, 비트 조작을 통해 최하위 비트의 '0'을 '1'로 바꾸거나 비트를 왼쪽으로 시프트하는 등의 조작을 고려할 수 있습니다.
- 범위 제한하기: 실제 필요한 범위 내에서만 탐색을 수행합니다. n이 특별히 큰 수에 대해 모든 계산을 수행하기보다는, 실제 가능한 '1'의 개수가 일치하는 첫 번째 수를 찾은 후 즉시 반복을 중단합니다.
위의 변경사항은 프로그램의 효율성을 크게 향상시키며, 큰 범위의 입력에 대해서도 빠르게 결과를 도출할 수 있게 도와줍니다. Integer.bitCount()를 사용하는 것은 이진 표현을 직접 계산하는 것보다 효율적이며, 자바 내부 구현에서 최적화가 잘 되어 있습니다.

와우다!
로직은 내가 처음에 짠 거랑 별 차이 없다고 생각한다.
그러나 Integer.bitCount() 이 놈이 너무 강력하다.
별 다른 설명이 필요가 없을 정도로 코드가 간단하니 이제 문제 푸는 방식 2를 보자.
class Solution {
public int solution(int n) {
int answer = 0;
int bn11s = countBits(n);
for (int i = n + 1; i <= 1000000; i++) {
int bn21s = countBits(i);
if (bn11s == bn21s) {
answer = i;
break;
}
}
return answer;
}
private int countBits(int number) {
int count = 0;
while (number > 0) {
count += number & 1; // 마지막 비트가 1인지 확인
number >>= 1; // 오른쪽으로 한 비트 시프트
}
return count;
}
}여기서는 countBits라는 커스텀 메서드를 사용한다.

여기서 사용된 countBits 함수는 정수의 이진 표현에서 1의 개수를 세는 기능을 수행합니다. 비트 연산자 &와 >>=를 사용하는 방법에 대해 자세히 설명드리겠습니다.
countBits 함수의 작동 원리
- 변수 초기화:
- int count = 0;: 1의 개수를 세기 위해 count 변수를 0으로 초기화합니다.
- 루프 조건:
- while (number > 0): 숫자가 0보다 큰 동안 루프를 계속 실행합니다. 숫자가 0이 되면 루프가 종료됩니다. 이진수에서 0이 되면 더 이상 세어야 할 1이 없다는 의미입니다.
- 비트 연산자 &:
- count += number & 1;: number & 1 연산은 number의 가장 낮은 비트(즉, 가장 오른쪽 비트)가 1인지 확인합니다. &는 비트 AND 연산자로, 두 비트 모두 1일 때만 결과가 1입니다. 따라서 이 연산의 결과는 number의 마지막 비트가 1이면 1, 아니면 0이 됩니다.
- 예를 들어, number가 5인 경우 이진수로는 101입니다. 101 & 001은 001이며, 이는 1입니다. 따라서 count는 1 증가합니다.
- 비트 오른쪽 시프트 연산자 >>=:
- number >>= 1;: >>= 연산자는 number를 오른쪽으로 1비트 이동시킵니다. 이는 기본적으로 number를 2로 나눈 것과 같습니다.
- 이 연산 후 number의 이진 표현은 한 비트씩 오른쪽으로 이동하며, 매번 마지막 비트가 사라집니다. 이로 인해 다음 루프에서 새로운 마지막 비트를 검사할 수 있습니다.
전체 프로세스 예시
number = 13인 경우를 고려해 보겠습니다. 13의 이진수는 1101입니다.
- 첫 번째 루프: 1101 & 0001 = 0001 (1, count = 1), number는 110이 됩니다.
- 두 번째 루프: 0110 & 0001 = 0000 (0, count는 그대로), number는 11이 됩니다.
- 세 번째 루프: 0011 & 0001 = 0001 (1, count = 2), number는 1이 됩니다.
- 네 번째 루프: 0001 & 0001 = 0001 (1, count = 3), number는 0이 됩니다.
루프가 종료되고 count는 3을 반환합니다. number = 13은 이진수로 1101이므로, 이진수 표현에서 1의 개수는 3입니다.
이 방식은 수학적 연산이나 복잡한 반복문 없이도 매우 효율적으로 숫자의 비트 중 1의 개수를 세는 방법을 제공합니다.
두 번째 방식은 코테에서 내가 절대 못 쓸 것 같다!
일단 이 건 여기서 끝!
결론: Integer.bitCount();
'코딩테스트 연습' 카테고리의 다른 글
| [묘공단] 너비 우선 탐색(BFS) (0) | 2024.05.19 |
|---|---|
| [묘공단] 깊이 우선 탐색(DFS) (0) | 2024.05.19 |
| 이진 변환 반복하기 (0) | 2024.05.12 |
| 최솟값 만들기 (0) | 2024.05.12 |
| 소수 찾기 (0) | 2024.05.12 |



